链表找环方法证明（拒绝误人子弟）

前言

今天又想起来了这个问题，之前最开始是在其他论坛中看到有人说起了这个面试题。

当时只是翻了下，大致了解了如何判断链表中是否有闭环，用两个快慢指针解决，但是没有了解如何去找到闭环开始的节点。

刚上网搜了下，一群垃圾博主乱七八糟胡说八道，就知道从其他地方复制粘贴，都不过脑子的。谁说较快指针一定就是第二次在环上移动就能遇到较慢指针的，我这么个渣渣都能一眼看出来毛病一群人还复制粘贴都说 2，你们还真是 2！

问题描述

一条链表如何判断是否有环？若是有环那怎么找到链表环的入口？

解决思路

先判断是否有环

思路：用快慢两个指针分别从链表头开始，慢指针 -> next，快指针 -> next -> next，这样如果有环那快指针务必会跑到慢指针后面，随即两者之间的距离一次会缩小一步，最终相遇。若是未相遇且快指针的 next 为 null，则说明链表无环。

若是有环怎么找到环入口

链表中有闭环即快慢两指针相遇了，见下方的手工图：

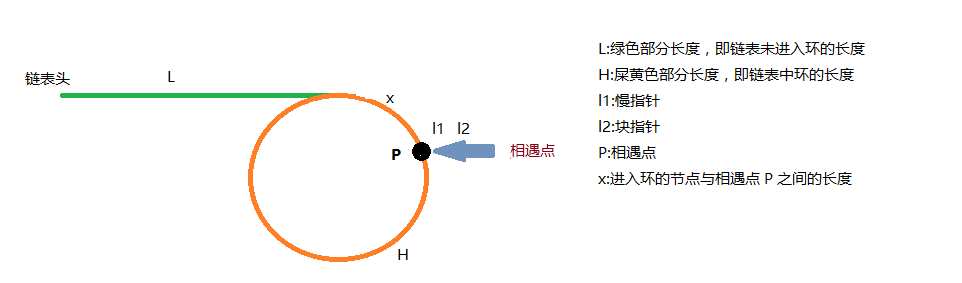
一切清晰明了。让我们再来捋一捋。

当两指针在 P 点相遇，我们可列出如下等式：

2(L+x) = L+x+n*H        (n >= 1) // n 为快指针在闭环上的圈数
=> 2L+2x = L+x+n*H      (n >= 1)
=> L = n*H-x            (n >= 1)
=> L = n*(H-x)+(n-1)x   (n >= 1)

到这里，是不是有种扒光了的快感，哈哈。
网上许多博客就是把 n 默认当成了 1，实则不然。

思路：故我们可以这样做，当 l1 与 l2 相遇时，再来一个 l3 指针从链表头开始，而 l1 继续走，l2 就可以终结其使命没必要继续走了。此时 l1 和 l3 指针都是指向其 next。当 l3 指针到达环入口时，l1 也必然到达了环入口，即 l1 和 l3 指针会在环入口相遇，从而可求得入口位置。

前言

问题描述

解决思路

参考博客